johngift.blogg.se - Lambda calculus beta reduction examples

#Lambda calculus beta reduction examples pdf
#Lambda calculus beta reduction examples archive
#Lambda calculus beta reduction examples plus

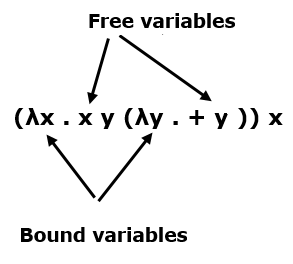
It's an extremely simple and basic thing. For example, the only thing lambda calculus lets you do is create terms consisting of symbols, single-argument anonymous functions, and applications of terms to each other (we'll look at the specifics soon). The big result in theoretical computer science is that these can all do the same thing, in the sense that if you can express a calculation in one, you can express it in any other.

Lisp, a human-friendly axiomatisation of computation that accidentally became an extremely good and long-lived programming language.

the projection functions, defined for all natural numbers a and b such that a \geq b as taking in a arguments and returning the bth one.

#Lambda calculus beta reduction examples plus

a successor function that takes a number and returns that number plus 1 and.

the zero functions, that take some number of arguments and return 0.

The partial recursive functions, constructed by function composition, primitive recursion (think bounded for-loops), and minimisation (returning the first value for which a function is zero) on three basic sets of functions:.

The lambda calculus ( λ-calculus), a formal system that has expressions that are built out of an infinite set of variable names using λ-terms (which can be thought of as anonymous functions) and applications (analogous to function application), and a few simple rules for shuffling around the symbols in these expressions.

moves one cell left or right on the tape.

transitions to some some state (possibly the same it is already in), and.

writes some symbol on the tape (possibly the same that was already there),.

given a combination of current state and current symbol on the tape, always does an action consisting of three things:.

has some set of states it can be in, some of which are termed "accepting" and one of which is the starting state and.

works on an infinite tape of cells from which a finite set of symbols can be read and written, and always points at one of these cells.

The Turing machine – that is, a machine that:.

At the end we will see a lambda calculus interpreter written in the lambda calculus, and realise that we're most of the way to Lisp.īut first, why care about lambda calculus? Consider four different systems: The goal is not to do maths with it, but rather to build up definitions within it so that we can express non-trivial algorithms easily. It is most useful if you want to get some intuition for the lambda calculus, or more generally for how simple axiomatisations of computation actually let you express anything.

#Lambda calculus beta reduction examples archive

&(f (\lambda x.\lambda y.x) \lambda g.This is a linkpost that I'm posting in response to a request to share more of the archive of my personal blog on LessWrong. It is written as a lambda calculus term L a m b d a L i s p = λ x. LambdaLisp is a Lisp interpreter written as a closed untyped lambda calculus term. is particulary interesting, consisting entirely of (s:

#Lambda calculus beta reduction examples pdf

Here is a PDF showing its entire lambda term, which is 42 pages long: LambdaLisp can be used to write interactive programs.Įxecution speed is fast as well, and the number guessing game runs on the terminal with an almost instantaneous response speed. Garbage collection during macro evaluation.Show the call stack trace when an error is invoked.Access to the interpreter’s virtual heap memory with malloc, memread, and memwrite.Object-oriented programming feature with class inheritance.Closures, lexical scopes, and persistent bindings with let.Universal Lambda interpreter clamb and Lazy K interpreter lazyk written by Kunihiko Sakamoto.The IOCCC 2012 “Most functional” interpreter written by John Tromp.The 521-byte lambda calculus interpreter SectorLambda written by Justine Tunney.When run on a lambda calculus interpreter that runs on the terminal, it presents a REPL where you can interactively define and evaluate Lisp expressions. The input and output text is encoded into closed lambda terms using the Mogensen-Scott encoding, so the entire computation process solely consists of the beta-reduction of lambda calculus terms. LambdaLisp is a Lisp interpreter written as an untyped lambda calculus term.